+ Our brand new course with The Dillinger Escape Plan’s Ben Weinman teaches how to make a living in music without making sacrifices. Check out The Business of Uncompromising Art, out now exclusively on Soundfly.
This article originally appeared on Ethan Hein’s blog.
Short answer: Because math.
Longer answer: Because prime numbers don’t divide into each other evenly.
When you pluck a guitar string, it vibrates to and fro. You can tell how fast the string is vibrating by listening to the pitch it produces. Shorter strings vibrate faster, and make higher pitches. Longer strings vibrate slower, and make lower pitches. The scientific term for the rate at which the string vibrates is its frequency. You measure frequency in hertz (Hz), otherwise known as vibrations per second. The standard tuning pitch, A440, is the pitch you get when your guitar string vibrates to and fro 440 times per second.
If you watch a slow-motion video of a guitar string vibrating, like the one above, you’ll see a complex, evolving blend of squiggles. Strings can vibrate in many different ways at once. In addition to the entire length of the string bending back and forth, the string can also vibrate in halves, in thirds, in quarters, and so on. These vibrations of string subsections are called harmonics, overtones, or partials.
The complicated squiggles you see in real-world string vibrations are the mathematical sum of all these different harmonics. Each harmonic produces a different pitch, so when you play a note, you’re actually hearing many different pitches at once. It’s possible to isolate the different harmonics of a string and hear their individual pitches. Harmonics are very useful for tuning your guitar. They are also the basis of the whole Western tuning system generally.
You isolate the harmonics on a guitar string by lightly touching it in certain places to deaden some of the vibrations. If you touch the vibrating string at its halfway point, you can hear it vibrating in halves. (On the guitar, the halfway point is right at the twelfth fret.) If you touch the string a third of the way along its length, you can hear it vibrating in thirds. (On the guitar, this point is right at the seventh fret.) Each whole-numbered fraction of the string produces a different harmonic. The shorter string sections produce higher and quieter harmonics.
Click this image below to hear the first six harmonics of a string:
The ancient Greeks figured out that if you have a bunch of strings, it sounds really good if you tune them according to the frequency ratios you get from the natural overtone series. In such tuning systems, you get all your notes by picking a starting frequency, and then multiplying or dividing it by whole numbers. The good-sounding (to Western people) note combinations are the ones derived from the lowest harmonics — the ones that have you multiplying or dividing by the smallest prime factors: two, three, and five.
Here’s a graphic representation of the lowest harmonics of a string tuned to C.
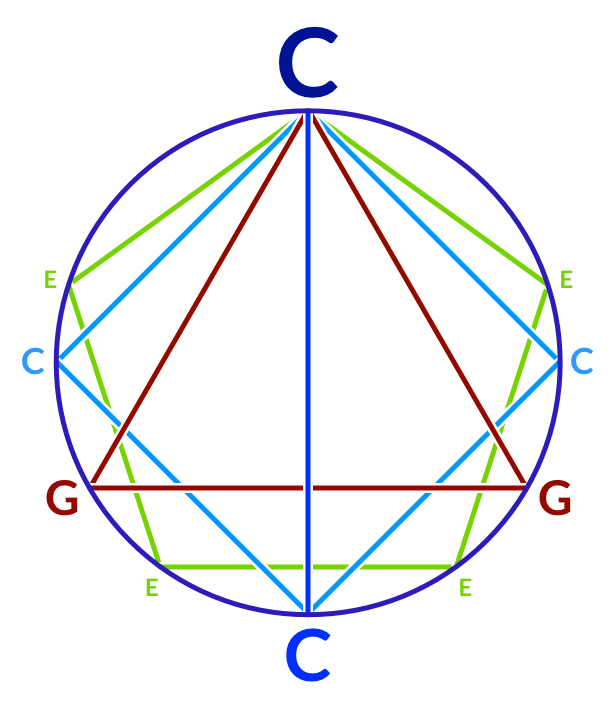
Let’s pretend that we have a guitar string tuned to play a note called middle C, which has a frequency of 1 Hz. (In real life, middle C has a frequency of 261.626 Hz, so if you want to think in terms of actual frequencies, just multiply all the numbers in the following paragraphs by 261.626.)
- The first harmonic is the string vibrating along its entire length, otherwise known as the fundamental frequency. When we say that our C string is vibrating at 1 Hz, that really means that its fundamental has a frequency of 1 Hz. The other harmonics all have other frequencies, and we’ll get to those, but the fundamental is the loudest harmonic, and usually it’s the only one you’re conscious of hearing.
- The second harmonic is the one you get from the string vibrating in halves. (Some people insist on calling this the first harmonic. Those people are wrong.) Each half of the string vibrates at twice the frequency of the whole string. The musical interval between the pitch of the entire string and the pitch of half of the string is called an octave. (I realize that the word suggests the number eight. You should ignore that for now.) The pitch that’s an octave above middle C has a frequency of 2 Hz, and it is also called C. (In scientific pitch notation, middle C is called C4, and the C that is an octave higher is called C5.) Both of these notes are called “C” because humans hear notes an octave apart from each other as being “the same.” This is probably because the notes share so many harmonics in common. The important concept here is that you can move up an octave from any pitch by doubling its frequency. You can also move down an octave from any pitch by halving its frequency.
- Let’s move on to the third harmonic, the one you get from the string vibrating in thirds. Its frequency is three times the fundamental frequency. Since our C string’s fundamental is 1 Hz, the third harmonic has a frequency of 3 Hz, and it produces a note called G.
- The fourth harmonic is the one produced by the string vibrating in quarters, at 4 Hz. This note is an octave higher than the second harmonic, and so is also called C. (The fourth harmonic is C6 in scientific pitch notation.) Are you noticing a pattern here? All the even-numbered harmonics are going to play Cs, at 8 Hz, 16 Hz, 32 Hz, 64 Hz, and at all the powers of 2 up to infinity.
- The fifth harmonic is the one produced by the string vibrating in fifths. Its frequency is 5 Hz, and it produces a note called E.
There are many more harmonics (infinitely many more, in theory) but these first five are the most audible ones, and they’re the only ones you need in order to build yourself a versatile tuning system.
So let’s do it. Let’s make a tuning system out of the harmonics of the C string. First, we should find the C, G, and E whose frequencies are as close to each other as possible. We’ve already got C at 1 Hz. We can bring our G at 3 Hz down an octave by dividing its frequency in half. This gives us a G at 3/2 Hz. We can also bring our E at 5 Hz down two octaves by dividing its frequency in half twice. This gives us an E at 5/4 Hz. When you play 1 Hz, 5/4 Hz and 3/2 Hz at the same time, you get a lovely sound called a C major triad. Cool!
It’s easy to make the rest of the notes in a C major scale just by combining our three existing intervals. Let’s start with D. If you know your music theory, you know that D has the same relationship to G that G has to C. Just like you can make a G by multiplying C’s frequency by 3/2, so too can you make your D by multiplying G’s frequency by 3/2. The interval between C and G, and between G and D, is called a perfect fifth. You can go up a perfect fifth from any note by multiplying its frequency by 3/2. So let’s go up a fifth from G at 3/2 Hz, multiplying it by 3/2 to get a D at 9/4 Hz. Then we can bring it down an octave by dividing its frequency in half, giving us a D at 9/8 Hz. So far, so good.
How about F? This one is easy too. The interval between F and C is also a perfect fifth. But this time we’re going down a fifth, not up. So to get down to F, we’re going to divide C’s frequency by 3/2, which gives us 2/3 Hz. We can then bring it up an octave by doubling its frequency, giving us an F at 4/3 Hz.
Okay, how about A? The interval between F and A, called a major third, is the same as the one between C and E. So we can go up a major third from F by multiplying 4/3 by 5/4 to get an A at 5/3 Hz. Alternatively, A is a perfect fifth above D, so we could just as easily multiply 9/8 by 3/2 to get… uh oh… 27/16 Hz. This is a problem. While 5/3 and 27/16 are pretty close to each other, they are not the same. Which one of these should we use? We’d ideally want the interval between D and A to be a perfect fifth (a multiple of 3/2), but if A is at 5/3 Hz, then it’ll clash pretty horribly with D at 9/8 Hz. On the other hand, we’d expect the interval between A to E to be a perfect fifth too. But if we go up a fifth from 27/16 Hz, we get 81/32 Hz, and if we move that down an octave to 81/64 Hz, we’ll be pretty close to E at 5/4 Hz, but not close enough.
Can you see the problem?
Anytime you want to use intervals based on perfect fifths, you’re multiplying and dividing by 3, but anytime you want to use intervals based on major thirds, you’re multiplying and dividing by 5. Starting from C, it’s possible to produce any note on the piano if you multiply or divide your frequencies by 3 enough times, but those notes won’t be in tune with the notes you’d get multiplying or dividing your frequencies by 5, because 3 and 5 don’t mutually divide evenly. This is not just an abstract mathematical issue. It’s the reason that it’s impossible to have a guitar be in tune with itself.
Let’s examine the guitar more closely. Imagine that the guitar’s low E string has a frequency of 1 Hz. (It’s really 82.4069 Hz; feel free to multiply everything in this next section by that number if you want actual frequencies.) You want your high E string to be tuned two octaves higher than the low one, at 4 Hz. Let’s see if you can get there by tuning the strings pairwise.
- The interval between E and A is a fifth, but it’s upside down, because we’re going down a fifth from A. In music theory terms, an upside down fifth is called a fourth. You go up a fourth by multiplying your frequency by 4/3 (it’s 3/2 upside down, doubled to bring it up an octave.) So your A string is now tuned to 4/3 Hz.
- The D string should be another fourth higher, so you can multiply by 4/3 again, giving you 16/9 Hz.
- The G string should be yet another fourth higher, so you multiply by 4/3 to get 64/27 Hz.
- The B string is a major third higher than G, which means multiplying by 5/4, and that puts you at 80/27 Hz.
- Finally, to get to high E, that’s another fourth, so you multiply by 4/3 again, giving you 320/81 Hz. This is not good. We wanted the high E to be at 4 Hz, also known as 324/81 Hz. We’re 4/81 Hz flat! That may not seem like a big difference, but it’s quite noticeable and annoying.
Let’s try a different strategy. I said you should tune the B string a major third above G, but you could just as easily tune the B string a fifth plus an octave above the low E string. So let’s go ahead and multiply 1 Hz by 3/2, and then double it, which gives you a B at 3 Hz. Now the B string sounds terrific against the low E at 1 Hz and the high E at 4 Hz.
Unfortunately, it’s going to be pretty sour against the G string at 64/27 Hz. So maybe you should just tune the G string a major third below your new B, at 12/5 Hz. Now the G and B strings sound great together, but the G is out of tune against the D string at 16/9 Hz. So maybe D should be a fourth below G… but then the D string will be out of tune against A. If you tune the A based on your new D, then it’ll be out of tune against the low E. And if you tune the low E based on your new A, then it’ll be out of tune against the high E. There’s just no way to win.
The basic awkwardness of harmonics-based tuning systems has caused musicians a lot of confusion and irritation over the years. Depending on your starting pitch, some intervals can be perfectly in tune, but others can’t be. And the more harmonically complex you want your music to be, the worse the tuning issues are going to get.
Over the past few hundred years, Western Europeans gradually figured out an alternative system to harmonics-based tuning, called 12-tone equal temperament (12-TET for short). It’s the system that the entire Western world uses today. The idea behind 12-TET is to have everything be pretty much in tune, which you accomplish by having everything be a little bit out of tune. Is this a worthwhile compromise? Let’s do the math and find out.
In 12-TET, you don’t define your intervals by tidy ratios of whole numbers. Instead, you divide up the octave into twelve equally-sized semitones (the interval between two adjacent piano keys or guitar frets). You then add semitones together to make all the other intervals. To go up a semitone from any note, you multiply its frequency by the 12th root of two. To go down a semitone from any note, you divide its frequency by the 12th root of two. If you go up by an octave (12 semitones), you’re multiplying your frequency by the 12th root of two 12 times, which works out to two.
That’s a perfect octave, hooray! Unfortunately, the other intervals in 12-TET don’t work so well.
A fifth in 12-TET is defined as seven semitones. Instead of multiplying your frequency by 3/2, you multiply by the 12th root of two seven times, which is about 1.498. That’s close, but not quite on the nose. Major thirds are worse in 12-TET. Instead of multiplying your frequency by 5/4, you multiply by the 12th root of two four times. That gives you 1.25992, which is not very close to 5/4 at all. Nevertheless, we as a civilization have collectively decided that we should just suck it up and live with everything sounding a little wrong. There are plenty of good reasons to!
All intervals in 12-TET are the same size, regardless of starting pitch. Furthermore, all keys are comprised of the same interval relationships, so they’re completely interchangeable. In 12-TET, you can hop around from one key to another at will without having to stop and retune everything. That is pretty awesome.
Convenient though it is, some musicians don’t want to accommodate a 12-TET, insisting instead that we continue to use pure intervals derived from harmonics the way God and Pythagoras intended. Harmonics-based tuning systems are collectively known as just intonation. This is a poetically apt term, because it implies fairness. By contrast, the implicit message of 12-TET is that life isn’t fair. As we’ve learned, just intonation systems give you some lovely pure intervals, but are severely limited otherwise. A few malcontents prefer alternative historical compromise tuning systems that make some keys sound better at the expense of others sounding worse. There are many such esoteric temperament systems, but none of them are in widespread use.

A few oddballs and nerds have explored tuning systems that use bigger prime numbers to generate finer pure intervals. Harry Partch used the primes up to 11 to make a tuning system that divides up the octave into 43 pure parts rather than 12 impure ones. You can try the Partch scale using the Wilsonic app or Audiokit Synth One. It’s extremely strange! But, I guess, it’s strange in a pure way?
Most likely, you’ll do what everyone else does, which is live with everything being a little out of tune. And if you’re a guitarist, you know that no matter how you tune your guitar, it won’t stay in tune for long anyway, so how much does any of this even matter?
There’s a joke among guitarists: We spend half our lives tuning, and the other half wishing we were in tune.
There are lots of reasons why tuning is hard. You might be hampered by a poorly made guitar, or by a guitar that’s not set up correctly, or by old, worn-out strings, or by changes in temperature or humidity, or just by a lack of patience or time. At least you can be secure in the knowledge that some of your tuning struggles are due to the basic unfairness of the universe, and not just the limitations of your ears or your equipment.
Rev Up Your Creative Engines…
Continue your learning with hundreds of lessons on songwriting, mixing, recording and production, composing, beat making, and more on Soundfly, with artist-led courses by Kimbra, RJD2, Com Truise, Kiefer, Ryan Lott, and Ben Weinman’s The Business of Uncompromising Art.




