
+ Combine theory, improvisation, and jazzy hip-hop, and improve your piano chops with Grammy-winner Kiefer in Kiefer: Keys, Chords, & Beats.
This article originally appeared on The Ethan Hein Blog.
I complain a lot on my blog about the traditional teaching of music theory. Fortunately, a better alternative exists: Everyday Tonality by Philip Tagg. Don’t be put off by the DIY look of the website; the book is the single best explanation I know of for how harmony works across a broad spectrum of the world’s music.

Tagg brings an ethnomusicological approach to music theory. Rather than starting with a particular theoretical approach and trying to fit it to different kinds of music, he tries to derive generalizations from different kinds of music as they are practiced. If his model is less tidy than the standard classical theory text, so is the world he’s trying to describe.
Euroclassical theory was invented to explain the Euroclassical canon, not every kind of music in the world. Even within that canon, the theory focuses on harmony to the exclusion of nearly everything else. The problem is that the academy teaches this narrow theory of a particular aspect of the music of a certain time and place as if it were the foundation for understanding any kind of music.
But while Euroclassical tonal theory might be adequate to explain large-scale linear harmonic structure over the course of sections and movements of classical works, it fails when you try to apply it to the static, loop-oriented harmonies and structures of most of the music we listen to.
Tagg gives the example of “La Bamba.”
On its face, the chord progression to “La Bamba” couldn’t be any simpler: I, IV, and V, over and over. Tonal theory looks at that and says: tonic, subdominant, dominant, repeat. But “La Bamba” doesn’t feel like a narrative of being at rest, then mild tension, then more extreme tension, then being at rest again. The chords go by too fast and with too many repetitions for that. The song isn’t a linear narrative; it feels more like one continuous mood. Tagg explains:
“Explaining something as common and as ostensibly simple as the ‘La Bamba’ chord loop (as in ‘La Bamba,’ ‘Guantanamera,’ ‘Wild Thing,’ ‘Pata Pata,’ ‘Twist & Shout,’ etc.) in terms of tonic, subdominant, and dominant had for some time struck me as about as productive as using theories of combustion to explain electricity. And, yet, some music scholars still try to apply Schenkerian notions of harmonic directionality to tonal configurations in which notions like ‘dominant’ and ‘perfect cadence’ are at best questionable, if not altogether irrelevant.”
Tagg argues that to understand the cyclical ambiance of groove-based harmony, we need a theory of “the extended present” (10), not of linear-narrative function. Euroclassical theory ignores metricity, periodicity, timbre, groove, and sonic staging. Those last three parameters are beyond the scope of Tagg’s project, but he does have some useful ideas about bringing meter and repetition into the study of harmony. One such is the idea of “one-chord changes,” as in Aretha Franklin’s “Chain of Fools.”
There’s only one chord in “Chain of Fools,” C minor, which makes it severely impoverished by classical harmony standards. But the song doesn’t feel boring or static when you hear it because it isn’t a single chord droning or mindlessly repeating. The tune is built from complex interlocking rhythmic figures that accent different parts of the chord and its extensions in different metrical positions. When you consider the way that these different pieces of C minor deploy to support the groove, you start to understand “Chain of Fools” as the rich and exciting piece of music that we all intuitively experience it to be.
Tagg’s next useful term is the “shuttle,” a groove that switches back and forth between two chords. One of his examples is the Gm7 to C7 groove in Pink Floyd’s “The Great Gig in the Sky.”
+ Learn more on Soundfly: Create more powerful, emotional experiences in your music by understanding harmonic theory. Our popular online course with one-on-one mentorship, Unlocking the Emotional Power of Chords, can help you get there quicker!
What key is this groove in?
Classical and jazz theory both say it’s a ii-V progression in F major. A more reasonable argument would say that F never appears, so, really, it’s a i-IV progression in G Dorian. Tagg thinks that neither description is correct, though he’d probably agree that the latter one is closer to the truth.
Instead, Tagg argues we should hear the groove as being in the “key” of Gm7/C7. Neither of those chords is “a place you pass on the way to another destination” — we need to understand them both as comprising “a tonical neighborhood” that “is itself somewhere to be” (377). Rather than a teleological pull to a single chord, whether it’s F major or G minor, there’s a unified “dynamic ongoing tonal state” (23). This is certainly the most accurate description of my mental approach to playing or writing a two-chord groove.
Tagg offers another way to think about two-chord shuttles: the idea of “dual tonicity” (426), two different modes with two different tonics coexisting in superposition. Even if the two chords have a V-I relationship (e.g., G7 and C), that doesn’t necessarily imply a dominant-tonic function. Instead, we might be hearing the simultaneous modes of G Mixolydian and C major. This is a common situation in Latin music, not to mention about half the pop songs currently on the radio.
“It should in short be understood that the V-I cadence does not trump all others in non-classical tonality and that reversal, partial or total, of harmonic direction… can establish two modes, each with its own tonic, inside the same short piece of music.” (439-440)
This reminds me of the way that West African drummers hear their rhythm patterns as being simultaneously in binary and triple meter. It’s no surprise, then, that African diasporic musical traditions would take a similarly ambiguous view of harmony.
Tagg sensibly uses the term “loop” for loops of three or four different chords. Chord function in loops is more a matter of metrical position than the contents of the chords themselves. When we talk about groove-based music, rather than using terms like dominant and subdominant, Tagg suggests we talk about the “outgoing chord,” the “medial chord,” and the “incoming chord.”
Each of these occupies a particular position in the metrical structure of the loop. The metrical functions of chord changes in a groove override whatever other functions the chords might suggest, whether they happen to be tonal, or modal, or blues, or seemingly random.
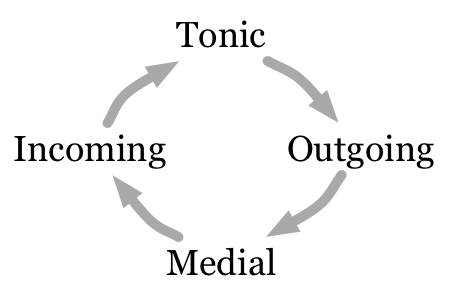
The loop might represent any length of musical time, depending on the harmonic rhythm. Each chord might last for two beats each, or one measure each, or two measures each, or whatever.
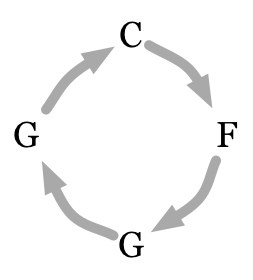
Using the loop concept, we can now make better sense of the “La Bamba” progression. The C chord is the tonic, the F is the outgoing chord, and G is both the medial chord and the incoming chord.
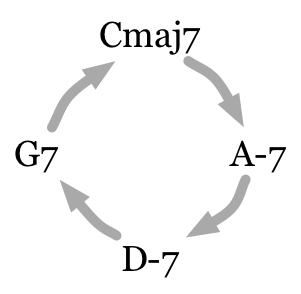
We can also understand a basic I-vi-ii-V jazz turnaround in these terms: Cmaj7 is the tonic, A-7 is the escape chord, D-7 is the medial chord, and G7 is the incoming chord. It so happens that you can explain this progression in functional harmony terms as well, but Tagg thinks it’s more correct to hear the chords as part of a single mood, not as markers in a linear narrative.
In the examples I’ve given so far, classical and jazz theory would agree with Tagg’s analysis of what the tonic chord is. For an example where they differ, consider Lynyrd Skynyrd’s “Sweet Home Alabama,” an endless loop of D7, C, and G. Classical theory says that this is an unambiguous dominant, subdominant, and tonic in G major. Besides, G major occupies twice as much time as either of the other two chords. Tagg’s theory says no; look at the metrical positions.
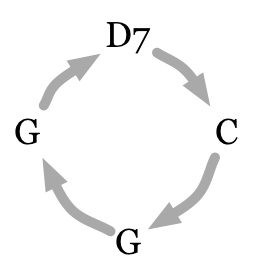
Since D7 occupies the tonic position, it must be the tonic chord. The tune is therefore in the “key” of D Mixolydian, not in G. Note that if we disregard rhythm, both “Sweet Home Alabama” and “La Bamba” are the “same” chords (if we transpose the latter up a fifth). Thinking about loop function shows us how they nevertheless describe different tonalities.
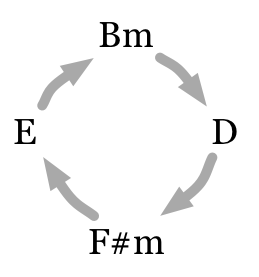
Here’s a tougher one: What key is Daft Punk’s “Get Lucky” in?
There are four chords here: B minor, D major, F-sharp minor, and E major. I can think of five different keys that these chords might plausibly imply.
- If B minor is the tonic chord, then the progression is i-III-v-IV. This puts us in B Dorian mode, though that’s only weakly established by the minor v chord.
- If D is the tonic chord, then the progression is vi-I-iii-II. This puts us in D Lydian mode, which is unlikely for a pop song. Besides, now there’s no dominant or subdominant chord.
- If F-sharp minor is the tonic chord, then the progression is iv-♭VI-i-♭VII. This puts us in F-sharp natural minor, which would be reasonable, except that now the tonic is in a metrically weak position.
- If E is the tonic chord, then the progression is v-♭VII-ii-I. This puts us in E Mixolydian mode, which also has a weak minor v chord.
- Since all of these scales are modes of A major, maybe that’s really the key. Maybe the progression is ii-IV-vi-V. This would make perfect sense, except how can A be the tonic chord if it never once appears in the song?
Tagg would say: We’re asking the wrong questions. The song is in all of these keys and none of them. The rules of functional harmony are no help. Instead, we should ask about the metrical function of the four chords. Using Tagg’s terminology, B minor is the tonic because it’s in the tonic position. D is the escape chord, F-sharp minor is the medial chord, and E is the incoming chord. If you were going to improvise a solo over these changes, you could use any of the five scales mentioned above. (They’re all the same seven pitches anyway.)
How about the chorus of Stevie Wonder’s “Sir Duke“?
The chords are B, Fm7, C#m7, and F#7. If you ignore the second chord, it’s a straightforward ii-V-I in B, but what the heck is going on with that Fm7? Tagg would say, Who cares? It’s the outgoing chord. The fact that the other three chords happen to be “functional” doesn’t make the Fm7 sound strange; in the context of Wonder’s groove, it sounds perfectly fine. You could really put any chords into the four slots as long as they don’t clash with the melody.

Not all repeated chord progressions are loops. Tagg argues that if the loop is longer than about 18 seconds, we’re more likely to hear it as a “cyclical matrix” like 12-bar blues or rhythm changes. I wonder if we couldn’t create a more complex diagram of circles within circles to better understand the metrical function of harmonies in those bigger forms, but that’s a question for another post.
Tagg shares my frustration with the Euroclassical world’s arrogance toward other music. Institutional theorists impose their own value system onto any other music they encounter in a casual act of aesthetic colonialism.
“[N]o-one in their right mind would dismiss Beethoven quartets (for example Op. 131 in C# minor) on grounds of monometricity (no cross-rhythms), monotimbrality (just a string quartet), or monospatiality (no variation of acoustic ambiance) because it’s obvious that the main dynamic of those quartets comes from thematic and harmonic development over time. By the same token it’s silly to dismiss Chuck Berry’s ‘Nadine’ because it spends 70% of its time on one chord, or Bo Diddley’s ‘Bo Diddley’ because it’s all on one chord.” (353)
Actually, plenty of people in their right minds do dismiss Beethoven for exactly those reasons. The vast majority of contemporary Western listeners strongly prefer music with cross-rhythms, varying timbres, and wildly diverse acoustic ambiances. We call that music rock, or hip-hop, or EDM, or reggae, or any of the other kinds of popular music descended from the African diaspora.
Too many music educators from Euroclassical culture sneer at the rest of us for our lack of interest in their music. These same educators too often show a shocking ignorance of the music that everyone else finds meaningful and enjoyable. We, the pop-oriented progressives, have our work cut out for us.
“The reform and de-ethnocentrification of music theory is an uphill battle in the context of institutions whose existence relies on musical traditions that have to be socially dead, or at least moribund, in order for them to become fixed as canons — for example, the euroclassical canon, the jazz canon, the ‘academic safari’ canon and, more recently, the rock canon.”
Canons are institutionally useful. It’s a pain to constantly have to be revising and updating curricula, textbooks, and exams. Nevertheless, if we’re going to teach music responsibly, we should at the very least be teaching it correctly. We should treat Euroclassical theory as the esoteric subspecialty that it is. If we’re going to impose a single, universally learned music theory on every student (and I don’t think we should), then I’d prefer it look more like Tagg’s.
Here’s that link again for Everyday Tonality if you’re interested, and of course, check out Tagg’s other books. Ten Little Title Tunes is particularly good.
Don’t stop here!
Continue learning with hundreds of lessons on songwriting, mixing, recording and production, composing, beat making, and more on Soundfly, with artist-led courses by Kimbra, Com Truise, Jlin, Ryan Lott, and the acclaimed Kiefer: Keys, Chords, & Beats.




